2019. 7. 16. 21:27ㆍAI/Deep Learning
이번 포스팅은 3층 신경망 구현에 대해서 정리하겠습니다.
3층 신경망에서 수행되는 입력부터 출력까지의 처리(순방향 처리)를 구현합니다.
이를 위해 numpy의 다차원 배열을 사용합니다.
1. 3층 신경망 구조

왼쪽부터 입력층(0층) 2개의 뉴런, 은닉층(1층) 3개의 뉴런, 은닉층(2층) 2개의 뉴런, 출력층(3층) 2개의 뉴런
으로 구성되어 있습니다.
2. 표기법
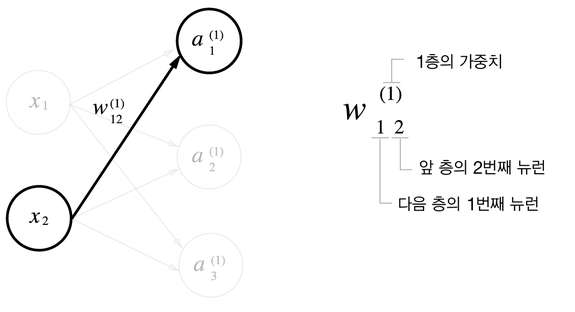
가중치와 은닉층 뉴런의 오른쪽 위에는 (1)이 붙어 있습니다. 이는 1층의 가중치, 1층의 뉴런임을 뜻하는 번호입니다.
또, 가중치의 오른쪽 아래의 두 숫자는 차례로 다음 층 뉴런과 앞 층 뉴런의 인덱스 번호 입니다.
예를 들어 1층의 1번째 뉴런에서 2층의 2번째 뉴런으로 가는 가중치라면 W21입니다.
그리고 2층으로 가는 것이기 때문에 (2)가 붙어서 최종적으로는 W21(2)가 되겠습니다.
3. 각 층의 신호 전달 구현하기

편향을 뜻하는 뉴런인 1이 추가되었고, 편향은 오른쪽 아래 인덱스가 하나밖에 없다는 것에 주의해야 합니다.
왜냐하면 앞 층의 편향 뉴런이 하나뿐이기 때문입니다.
지금까지 확인한 것을 수식으로 나타내보면 다음과 같습니다.

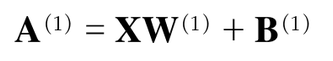
1) 입력층에서 1층으로의 신호 전달

x, w, b를 임의의 값으로 설정하여 진행하겠습니다.
|
1 2 3 4 5 6 7 |
X = np.array([1.0, 0.5]) W1 = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]]) B1 = np.array([0.1, 0.2, 0.3])
A1 = np.dot(X, W1) + B1 # [0.3 0.7 1.1]
Z1 = sigmoid(A1) #[0.57444252 0.66818777 0.75026011] |
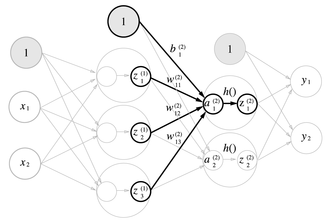
2) 1층에서 2층으로의 신호 전달
|
1 2 3 4 5 6 7 |
W2 = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]]) B2 = np.array([0.1, 0.2])
A2 = np.dot(Z1, W2) + B2 # [0.51615984 1.21402696] Z2 = sigmoid(A2) # [0.62624937 0.7710107 ] |
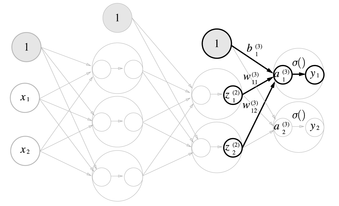
3) 2층에서 출력층으로의 신호 전달
|
1 2 3 4 5 6 7 8 9 |
def identity_function(x): return x
W3 = np.array([[0.1, 0.3], [0.2, 0.4]]) B3 = np.array([0.1, 0.2])
A3 = np.dot(Z2, W3) + B3 # [0.31682708 0.69627909] Y = identity_function(A3) # [0.31682708 0.69627909] # Y = A3 |
여기서 항등 함수인 identity_function()을 정의하고, 이를 출력층의 활성화 함수로 이용했습니다.
항등 함수는 입력을 그대로 출력하는 함수입니다.
그래서 identity_function을 굳이 정의할 필요는 없으나, 그 동안의 흐름과 통일하기 위해 구현했습니다.
또한 출력층의 활성화 함수는 시그마로 표시하여 은닉층의 활성화 함수 h()와는 다름을 명시했습니다.
4. 구현 정리
지금까지 구현한 것을 정리해보겠습니다.
신경망 구현 관례에 따라 가중치만 대문자로 작성하고, 편향과 중간 결과 등은 모두 소문자로 작성했습니다.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
def init_network(): network = {} network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]]) network['b1'] = np.array([0.1, 0.2, 0.3]) network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]]) network['b2'] = np.array([0.1, 0.2]) network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]]) network['b3'] = np.array([0.1, 0.2])
return network
def forward(network, x): W1, W2, W3 = network['W1'], network['W2'], network['W3'] b1, b2, b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x, W1) + b1 z1 = sigmoid(a1) a2 = np.dot(z1, W2) + b2 z2 = sigmoid(a2) a3 = np.dot(z2, W3) + b3 y = identity_function(a3)
return y
network = init_network() x = np.array([1.0, 0.5]) y = forward(network, x) print(y) # [0.31682708 0.69627909] |
출처:
밑바닥부터 시작하는 딥러닝(한빛미디어, 사이토 고키 지음, 개앞 맵시 옮김)
그림 1~6 / 식1,2:
'AI > Deep Learning' 카테고리의 다른 글
| [cs231n] Lecture 4. Introduction to Neural Networks (0) | 2019.07.27 |
|---|---|
| 신경망(1) 활성화 함수 (0) | 2019.07.16 |
| 다층 퍼셉트론 (0) | 2019.07.16 |
| 단층 퍼셉트론 (0) | 2019.07.16 |
| [cs231n] Lecture3. Loss Functions and Optimization (0) | 2019.07.16 |